Hyperbolic Space? Why do we care?

We normally see things from a Euclidean Geometry, and it has served us well. Why would we need Hyperbolic Geometry?

Let's say we have a tree with branching factor 3 and that is of depth 3. It would like the following
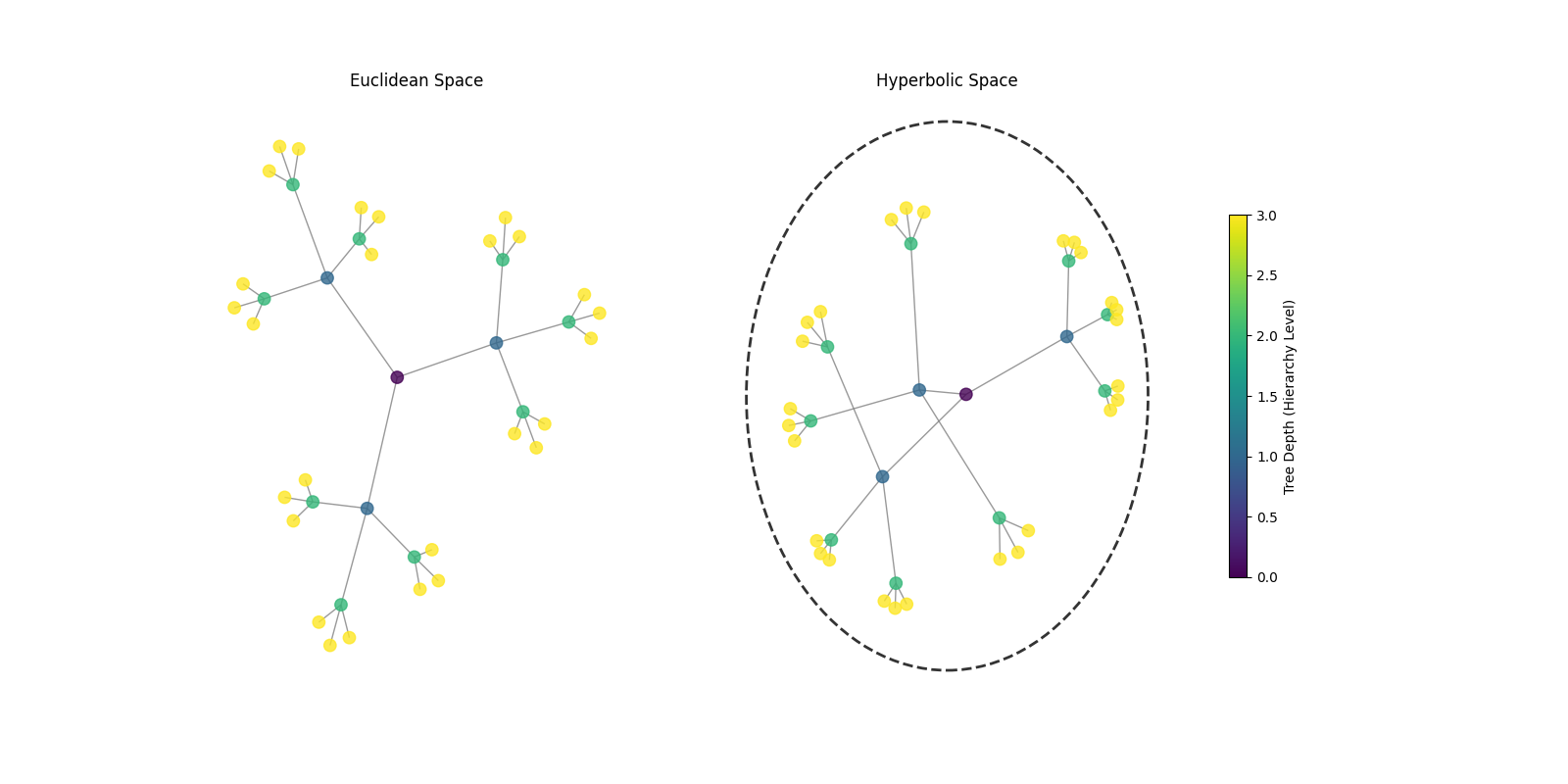
Figure_1 1.png

It looks similar in both, and the nodes that are further down the tree are towards the edge from the center.
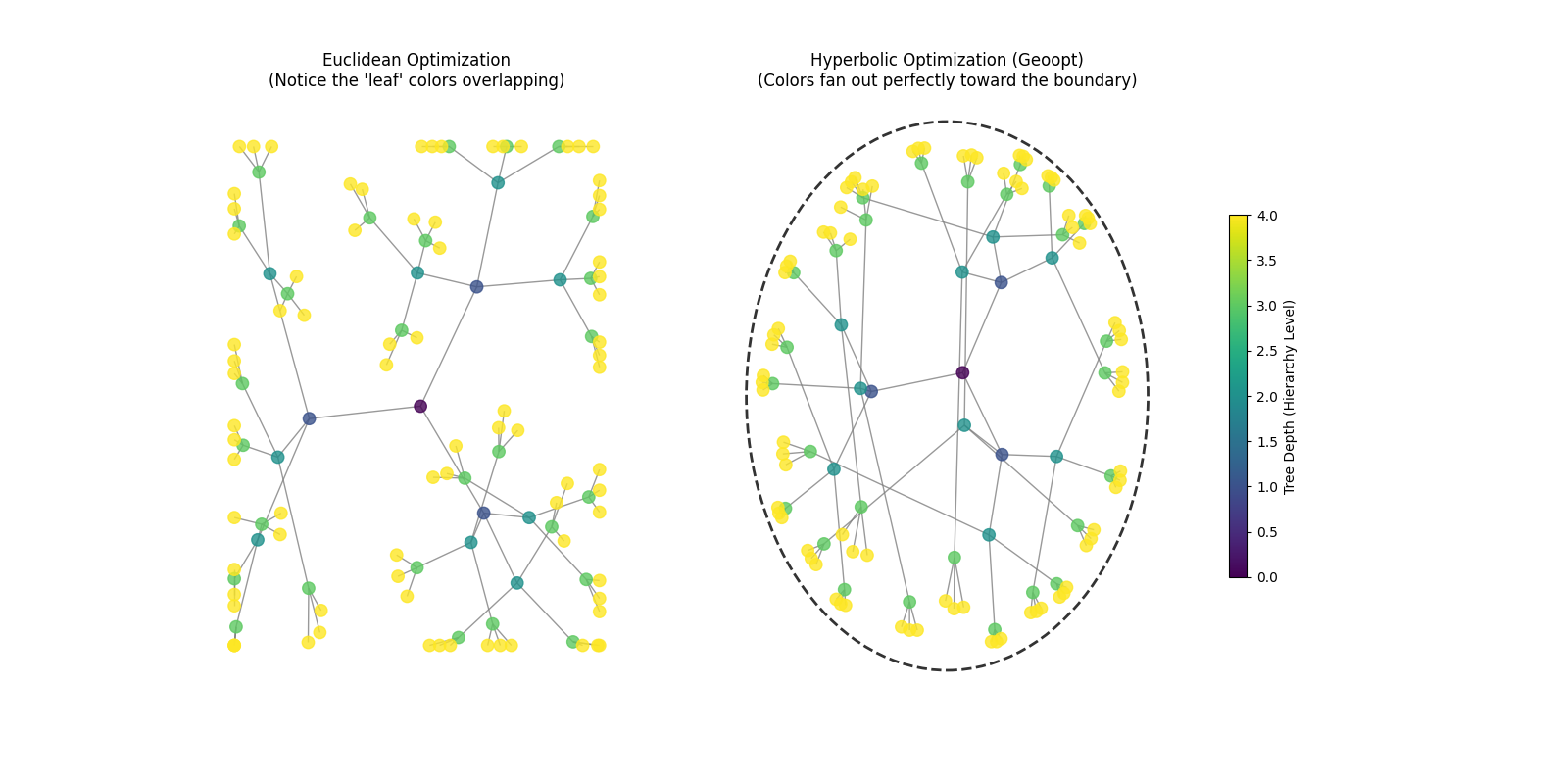
Now what if we increase the depth of the tree
For Depth=4

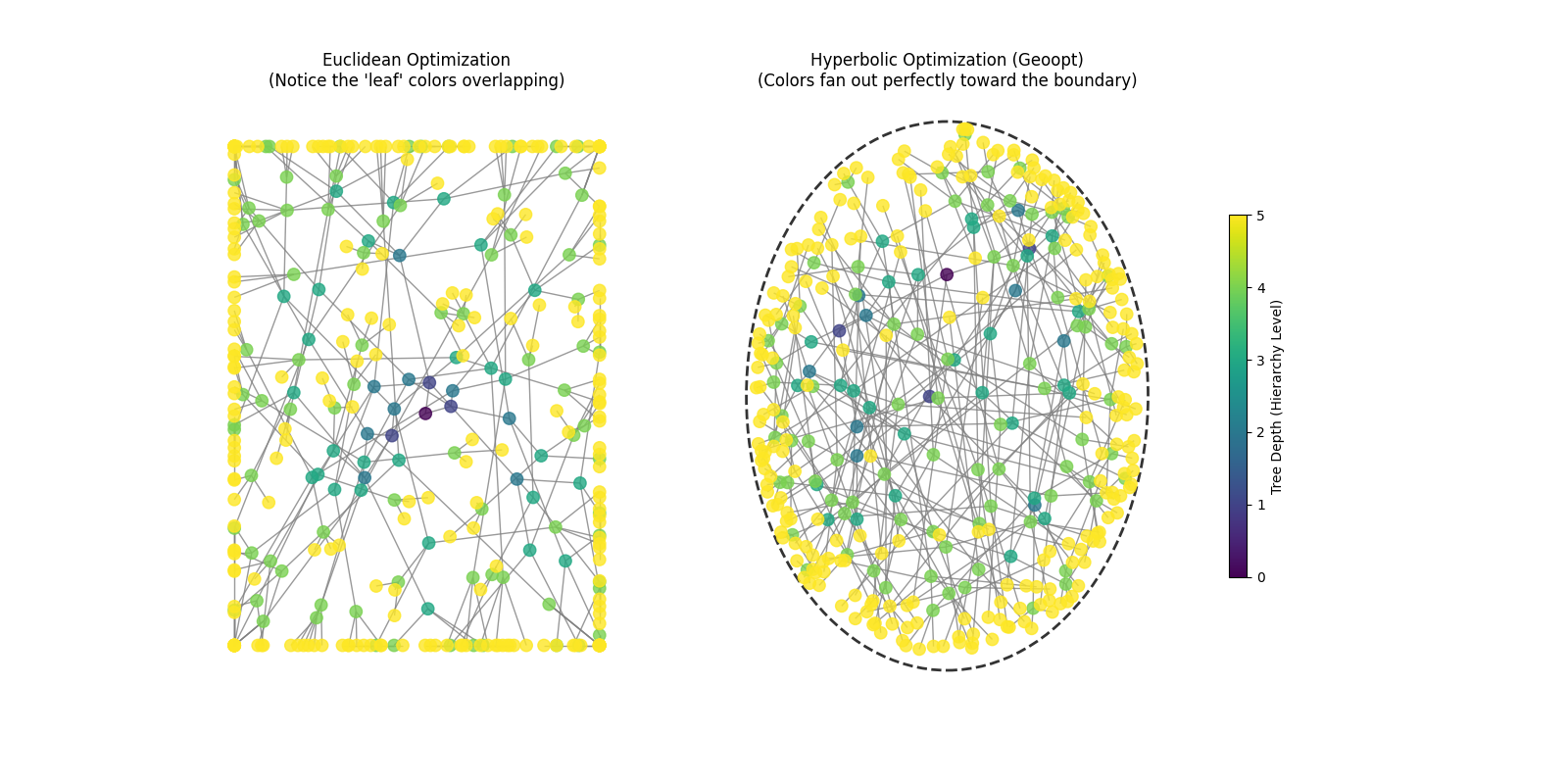
For Depth=5
Figure_1 2.png
For Depth=6

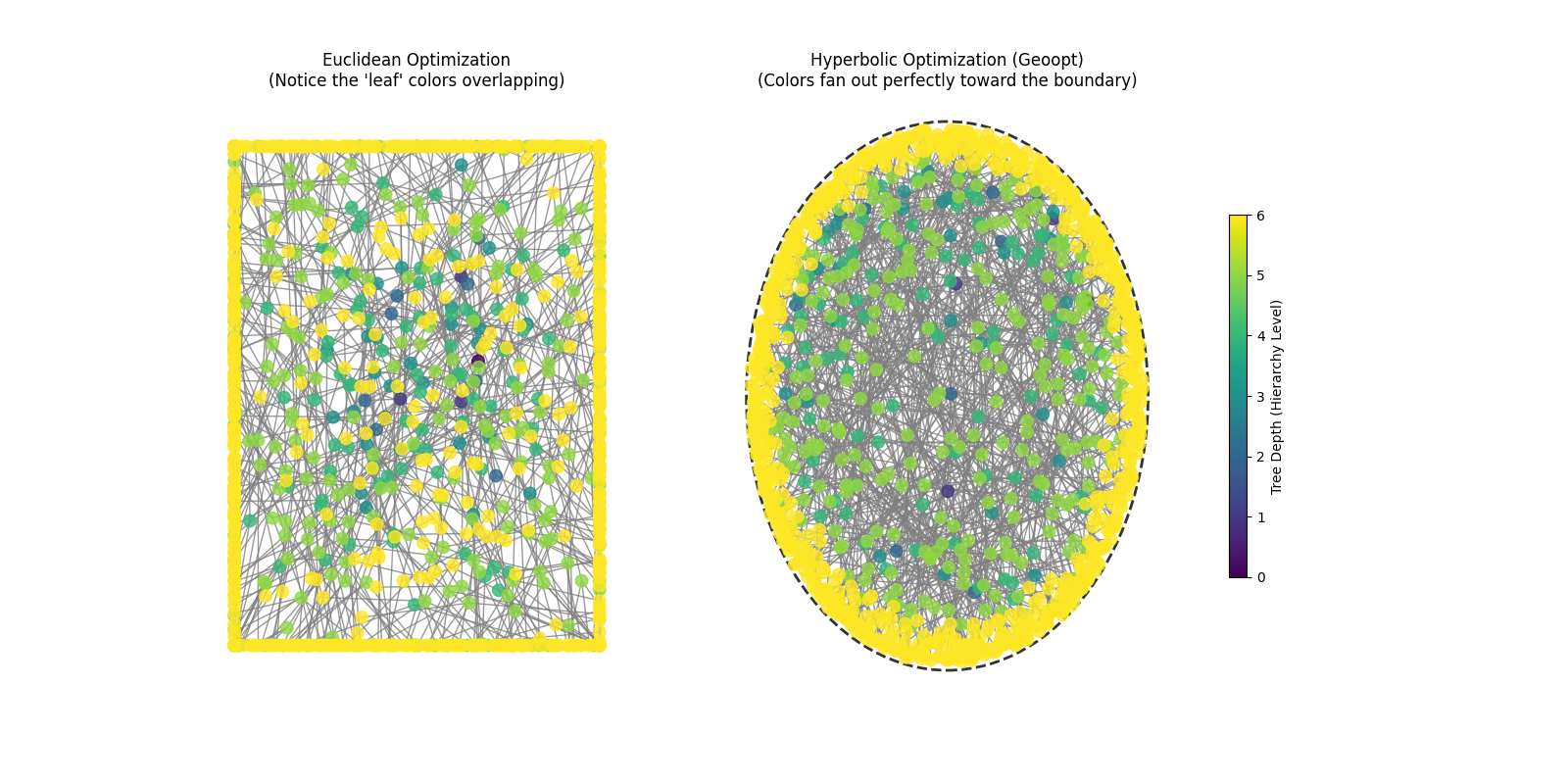
In Euclidean Space, the circumference grows linearly with the distance from the center, and the area grows quadratically with the distance from the center. However, a hierarchical tree grows exponentially as you increase depth, therefore the nodes overlap in a euclidean space.

In a Hyperbolic Space, the area and circumference grows exponentially. That is why, we are able to accomodate the growing nodes without overlapping them.

Why the area and circumference grows exponentially?

Negative Curvature

Curvature is simply how much something bends. It is quite intuitive in the 1D case, i.e a line that bends. How about a 2D surface? It can bend in many directions. Therefore, we define something called principal curvatures for a point on a surface.
They are the maximum and the minimum curvatures measured based on the point and they are represented by

\begin{array}{r} k 1 - M a x i m u m \\ k 2 - M i n i m u m \end{array}

Based on the principal curvatures, we define Gaussian Curvature as the product of these two principal curvatures.

In an Euclidean Space - We have Zero Gaussian Curvature, while in a Spherical Space, we have positive gaussian curvature, and in a Hyperbolic Space, we have a negative gaussian curvature.

What this means? If you have two parallel lines, they never intersect if your curvature is zero. They will always eventually converge if they have positive curvature, but they will diverge if they have negative curvature. This diverging behavior causes the area and the circumference to grow exponentially.

How to model this?

As we have realized, we can't exactly show/think of the hyperbolic space within an Euclidean framework, we need to have models that help us. Based on how we represent the space, we get several models. Some of them are Klein, Upper Half-Space and etc.

The model used to visualize in the above images is called Poincare Model

Poincare Model

The Key idea in the Poincare Model is that the points close to the boundary are infinitely far away from the center. The Model embeds all points within a unit ball of d-dimensions.

The space is defined as follows

B^{d} = {x \in R^{d} | | | x | | < 1}

The magic lies in the definition of the Riemannian Metric of the Model

It is defined as

g_{p} (x) = λ_{x}^{2} g_{e} (x)

where
$g_{p} (x) - R i e m a n n i a n M e t r i c i n P o i n c a r e M o d e l$
$g_{e} (x) - S t a n d a r d E u c l i d e a n D o t P r o d u c t$
$λ_{x} - C o n f o r m a l f a c t o r$

Conformal Factor is calculated using

λ_{x} = \frac{2}{1 - | | x | |^{2}}

Conformal Factor is the amount by which we rescale the lengths. A metric change is conformal if it preserves angles and only scales the lengths.

What is a Riemannian Metric?
It is an inner product of the tangent space at every point. A tangent space is a locally flat space that is associated with every point in the non euclidean space. Based on this tangent space, we define an inner product, so that we will be quantify distances and angles.

Poincare Model is very useful for visualizations, but it is not numerically stable. Therefore, we (the citizens of DL-land :) ) prefer a more numerically stable model and that is Lorentz Model

Lorentz Model

For a d-dimensional euclidean space, the Lorentz model is basically a two sheeted hyperboloid that exists in d+1 dimensional minkowski space and metric.

What is a Minkowski Space? A space that merges a time component with the spatial components.

The Metric here is defined as

< x, y >_{L} = - x_{0} y_{0} + Σ_{i = 1}^{d} x_{i} y_{i}

Using this metric, we can define the Hyperbolic Space as

H^{d} = {x \in R^{d + 1} | < x, x >_{L} = - 1, x_{0} > 0}

The distance between two points in the Lorentz Model is given as

d_{H} (x, y) = c o s h^{- 1} (- < x, y >_{L})

Before we answer the question as to why Lorentz Model is preferred for ML Optimization and Training, we have to first understand a few definitions

Geodesics, LogMap and Exponential Maps

Let's start with Geodesics.

Geodesics can be defined in two ways

It is the shortest path between two points on a surface, taking into account the local geometry. Like for example, a transatlantic would go towards north because it follows a geodesic of the spherical earth
A curve is a geodesic if its covariant acceleration is zero. That is just, math lingo for saying, when you walk along the curve, you will never actually change direction and just feel like walking straight.

We have briefly touched upon tangent space. We can think of tangent space as the best linear approximation at a point. How do we go back and forth from the tangent space to the hyperbolic space.

The Exponential Map answers the question "Given that I start at a point p and start walking in a direction of a tangent vector v, along a geodesic, where do I end up?"

Formally,

e x p_{p} (v) = γ_{v} (1)

where
$γ_{v} (t) - u n i q u e g e o d e s i c$
$γ_{v} (0) = p$
$γ_{p}^{.} (0) = v$

The LogMap is basically the inverse of the expmap. It answers the following question - "Given two points p and q, what tangent vector at p points towards q, and how far is q from p?"

Formally,

l o g_{p} (q) = v s . t e x p_{p} (v) = q

In Lorentz Model, logmaps, expmaps and geodesics have closed form solutions and that is why, we prefer the Lorentz Model for Optimization and Machine Learning.

Why do we (again, we are the citizens of the DL-land) care about them? We need them to perform our well-known optimization algorithms like SGD and others.
(Note: Optimization Algorithms in Deep Learning covers all the commonly used optimization algorithms.)

Riemannian SGD

How do we perform the well known "Stochastic Gradient Descent" in a Riemannian Manifold, like in a hyperbolic space?

We calculate the Riemannian gradient which is our traditional Euclidean Gradient projected to the tangent space of the manifold.
Give a learning rate, we take a step in the opposite direction in the tangent space
When we move in the tangent space, we would move away from the actual manifold. We map back from the tangent space to Manifold, using the expmap.

What's Next?

Hyperbolic Space has been used as a embedding space in NLP and CV, due to the ability to represent hierarchies. There have been techniques developed to quantify how hierarchical a dataset is.

This is just a starting point to understand how amazing Hyperbolic Space is.