The scale of model => One of the most important axes for better model quality.

Given a fixed computing budget, training a larger model for fewer steps is better than training a smaller model for more steps.

MoE => allows model to be pre-trained with far less compute and achieves good quality faster. It also allows model to learn varied knowledge

In the context of transformer models, MoE consists of two main elements

1. Sparse MoE layers => Used instead of dense feed-forward FFN layers. It has a certain number of experts, where each expert is a neural network (Usually experts are FFNs, but they could be anything.)
2. A gate network or router => Determines which tokens are sent to which expert. The router is composed of learned parameters and is pre-trained at the same time as the rest of the network

Challenges -
3. Historically struggled to generalize during fine-tuning, leading to overfitting.
4. Even though a MoE has a lot of params, only some of them are used during inference, leading to good speeds, but still we have to load all the params in memory.

For example, given a MoE like Mixtral 8x7B, we’ll need to have enough VRAM to hold a dense 47B parameter model. Why 47B parameters and not 8 x 7B = 56B? That’s because in MoE models, only the FFN layers are treated as individual experts, and the rest of the model parameters are shared. At the same time, assuming just two experts are being used per token, the inference speed (FLOPs) is like using a 12B model (as opposed to a 14B model), because it computes 2x7B matrix multiplications, but with some layers shared (more on this soon).

Basic Design of MoEs

Gating Function

Responsible for determining how the input data is allocated to designated experts.

The input data should be evenly distributed across the experts.

Most models use a Linear Gating Mechanism

Linear Gating

Linear Function with Softmax aka Softmax Gating

The softmax and the TopK operations are interchangeable. They both have their own pros and cons. Computing TopK first, filters out a lot of elements, reducing computational load. However, it might require additional normalization. In the other approach, we can use the activation weights to find $k$ for TopK.

Non-Linear Gating

[@chiRepresentationCollapseSparse2022] showed that linear gating reduced the representation capacity of Transformers. Given we use N experts, the authors show that the hidden vectors are represented in a N-dimensional subspace instead of representing them in a d-dimensional space where d is the dimension of the vector. They also found that it encourages the hidden states are routed to same expert.

To fix it,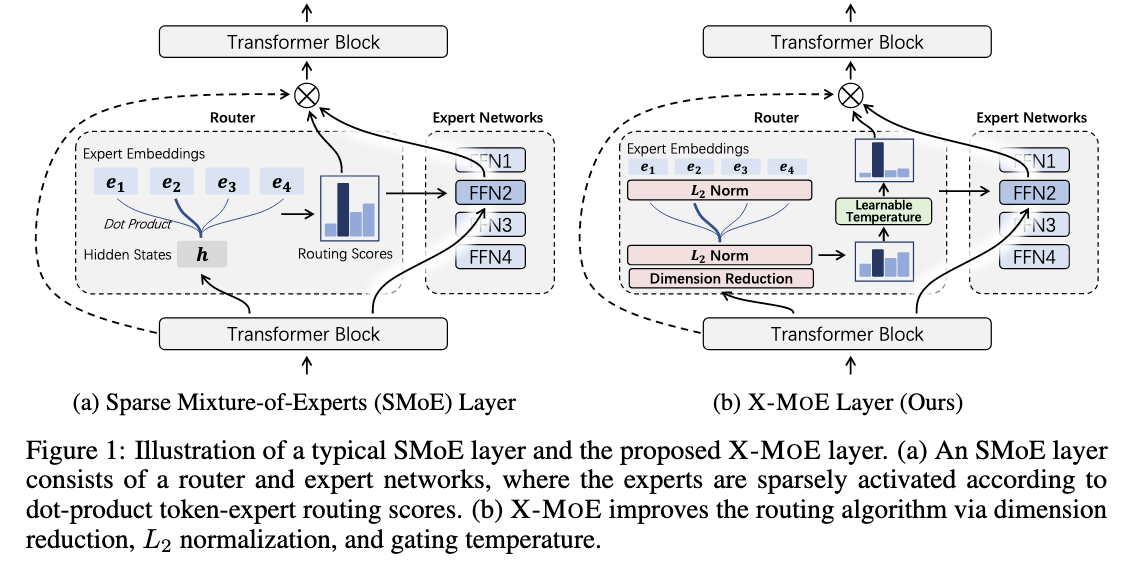
(Image taken from [@chiRepresentationCollapseSparse2022])

First they project the token vector into a low dimensional space and then normalize it so that the model don't just exploit a large embedding value to route all the tokens to the same token. The authors also divide a scores with a learnable Temperature parameter, thus the model could explore a lot more at the early stages of training and exploit later. This produces the scores for each experts $s_k$.

[@chiRepresentationCollapseSparse2022] showed that this router works better at multilingual tasks.[@liSparseMixtureofExpertsAre2023] shows that cosine router excels at handling cross-domain data.

The gating function could use soft-max or sigmoid based on the needs and it is given as follows:

There are also functions that uses the exponential family of Distribution to calculate the scores, instead of using cosine similarity.

Forget Routing and just use a weighted combination of all the experts

MoEs suffer issues such as Token Dropping, i.e some tokens are not processed by any expert. This happens if the number of tokens to an expert is more than the expert capacity - (The total number of tokens to be processed by each expert). Expert Capacity is introduced to make sure that an individual expert doesn't process all the tokens.

[@puigcerverSparseSoftMixtures2024] calculates weights between each token and each expert and uses those weights to do an weighted averaging of the outputs from each of the experts.

Expert Network

FFN is usually replaced because the FFN layers exhibit sparsity as a lot of neurons will not be activated simultaneously in the Transformer.

Level of Routing Strategy

Token-Level Routing

Determines Routing Decisions based on Token Representation

For Text Tokens, [@suMaskMoEBoostingTokenLevel2024] suggests to mask some experts randomly. For frequent tokens, it allows multiple experts to learn them. However, for infrequent tokens, it is routed to a single expert.

For Image Tokens, [@riquelmeScalingVisionSparse2021] suggested to send the patch tokens to routers in terms of importance. They called it Batch Priority Routing.

Modality Level Routing Strategy

History of MoEs

Roots - 1991, Adaptive Mixture of Local Experts

Between 2010-2015,

• Experts as components - In the traditional MoE setup - the whole system comprises a gating network and multiple experts. While https://arxiv.org/abs/1312.4314 - introduced the idea of it being components in deep models
• Conditional Computation

Sparsity

Idea of Conditional Computation. However this introduces some challenges, although large batch sizes are usually better for performance, batch sizes in MOEs are effectively reduced as data flows through the active experts. It could lead to uneven batch sizes and underutilization.

A simple Linear Layer with Softmax activation is used as the gating network

How to load balance tokens for MoEs? If all our tokens are sent to just a few popular experts, it makes training inefficient. In a normal MoE training, the gating network converges to mostly activate the same few experts. This self-reinforces as favored experts are trained quicker and hence selected more. To mitigate this, an auxillary loss is added to encourage giving all experts equal importance. There is also the concept of expert capacity => Introduces a threshold of how many tokens can be processed by an expert.

MoEs and Transformers

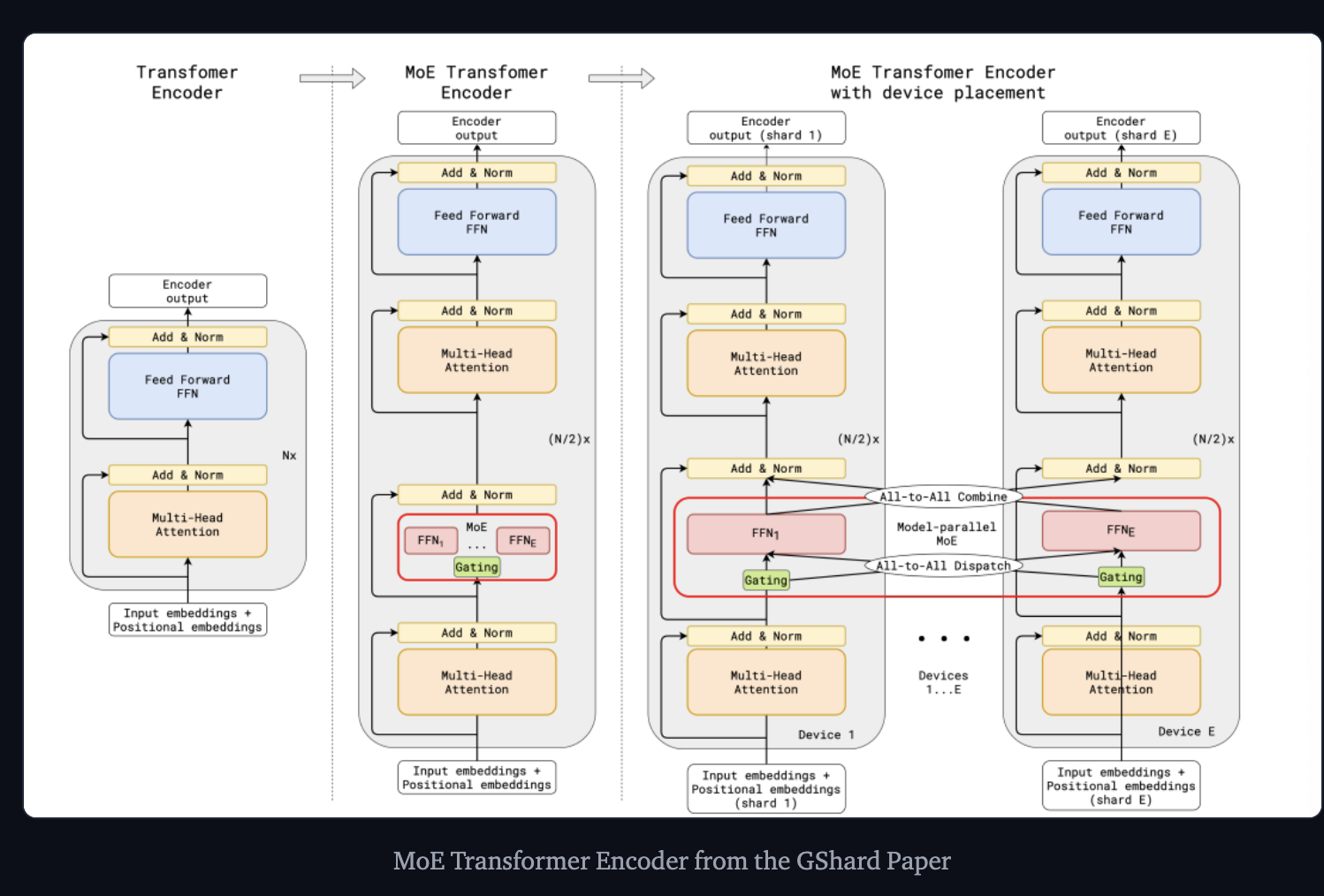
Google GShard - which explores scaling up transformers beyond 600 billion parameters. - Replaces every other FFN layer with an MoE layer using top-2 gating in both the encoder and the decoder.

When scaled to multiple devices, the MoE layer can be just shared across devices while all the other layer can be replicated.

In a top-2 setup, we always pick top expert, but the second expert is picked with a probability proportional to its weight.

Expert capacity - Set a threshold of how many tokens can be processed by one expert. If both experts are at capacity, the token is consdiered overflowed, and its sent to the next layer via residual connections.

GShard Paper => Also talks about parallel computation patterns that work well for MoEs

Switch Transformer Paper => The authors replaced the FFN layers with a MoE layer => Receives two inputs (two different tokens) and has four experts.

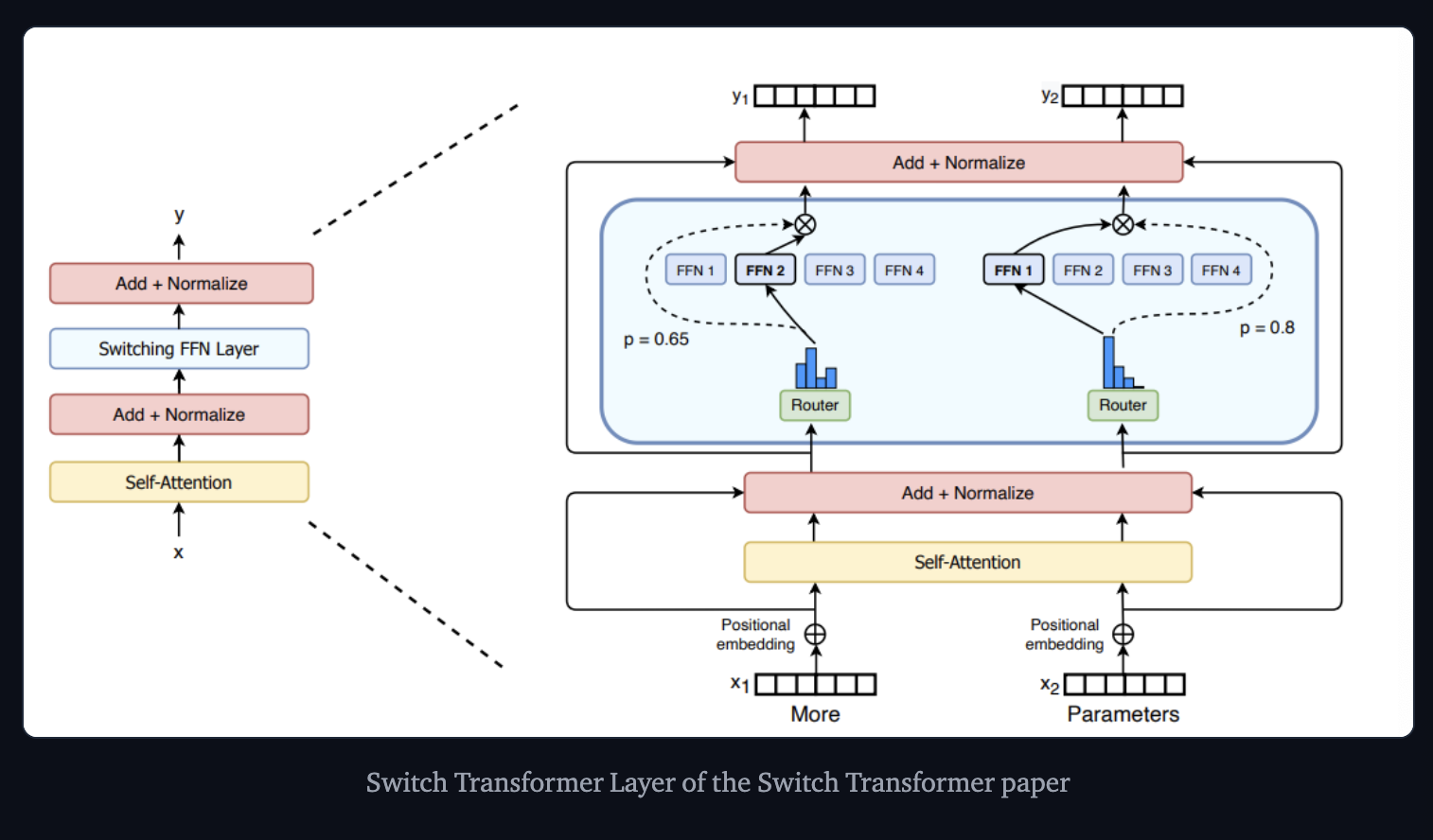
Switch Transformer uses just a simplified single-expert strategy, causing the following

1. The router computation is reduced
2. The batch size of each expert can be at least halved
3. Communication costs are reduced
4. Quality is preserved.

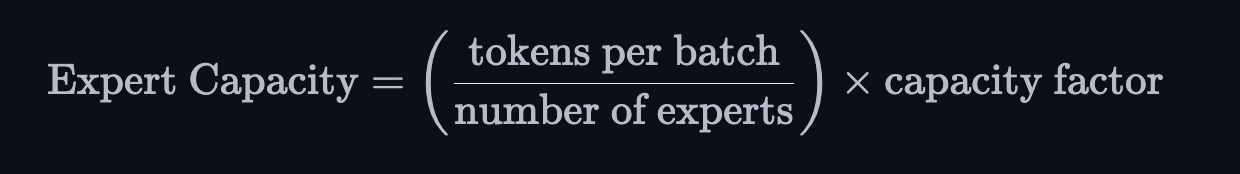
If we use a capacity factor greater than 1, we provide a buffer for when tokens are not perfectly balanced, However increasing the capacity will lead to more expensive inter-device communication, so it's a trade-off to keep in mind.

For each Switch Layer, the auxillary loss is added to the total model loss during training. The authors also used selective precision (i.e use bfloat16 for MoE layers and float32 for other layers).
However, the load balancing auxillary loss could lead to instability issues. At the expense of quality, we can stabilize training, by introducing dropout.

In ST-MoE, Router z-loss is introduced which significantly improves training stability without quality degradation by penalizing large logits entering the gating network.

What does an expert learn?

Encoder experts specialize in a group of tokens or shallow concepts (i.e proper noun expert, punctuation expert and so on). On the other hand, the decoder experts have less specialization.

The authors of St-MOE also noticed that when trained in a ultilingual setting, instead of specializing in a language, there is noting like that

Scaling w.r.t number of experts

More experts lead to improved sample efficiency and faster speedup but these are diminishing gains (especially after 256 or 512).

Fine-tuning MoEs

Sparse models are more prone to overfitting - so we can explore higher regularization within the experts themselves.

Whether to use the auxillary loss for fine-tuning? The ST-MoE authors experimented with turning off the auxiliary loss, and the quality was not significantly impacted, even when up to 11% of the tokens were dropped. Token dropping might be a form of regularization that helps prevent overfitting.

The authors of Switch Transformers observed that at a fixed pretrain perplexity, the spare model does worse than the dense counterpart in downstream tasks, especially on reasoning heavy tasks. However on knowledge heavy tasks it performs disproportionately well.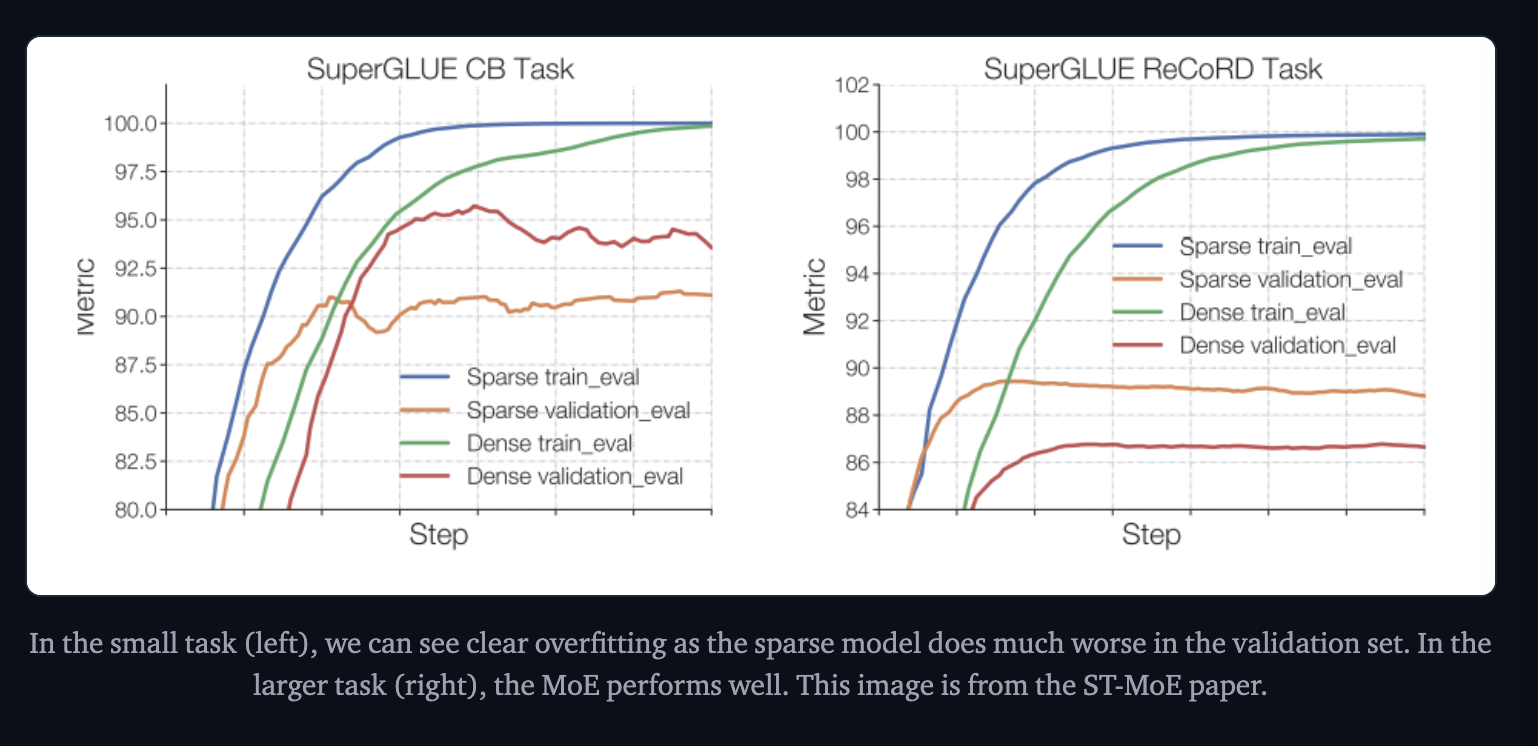

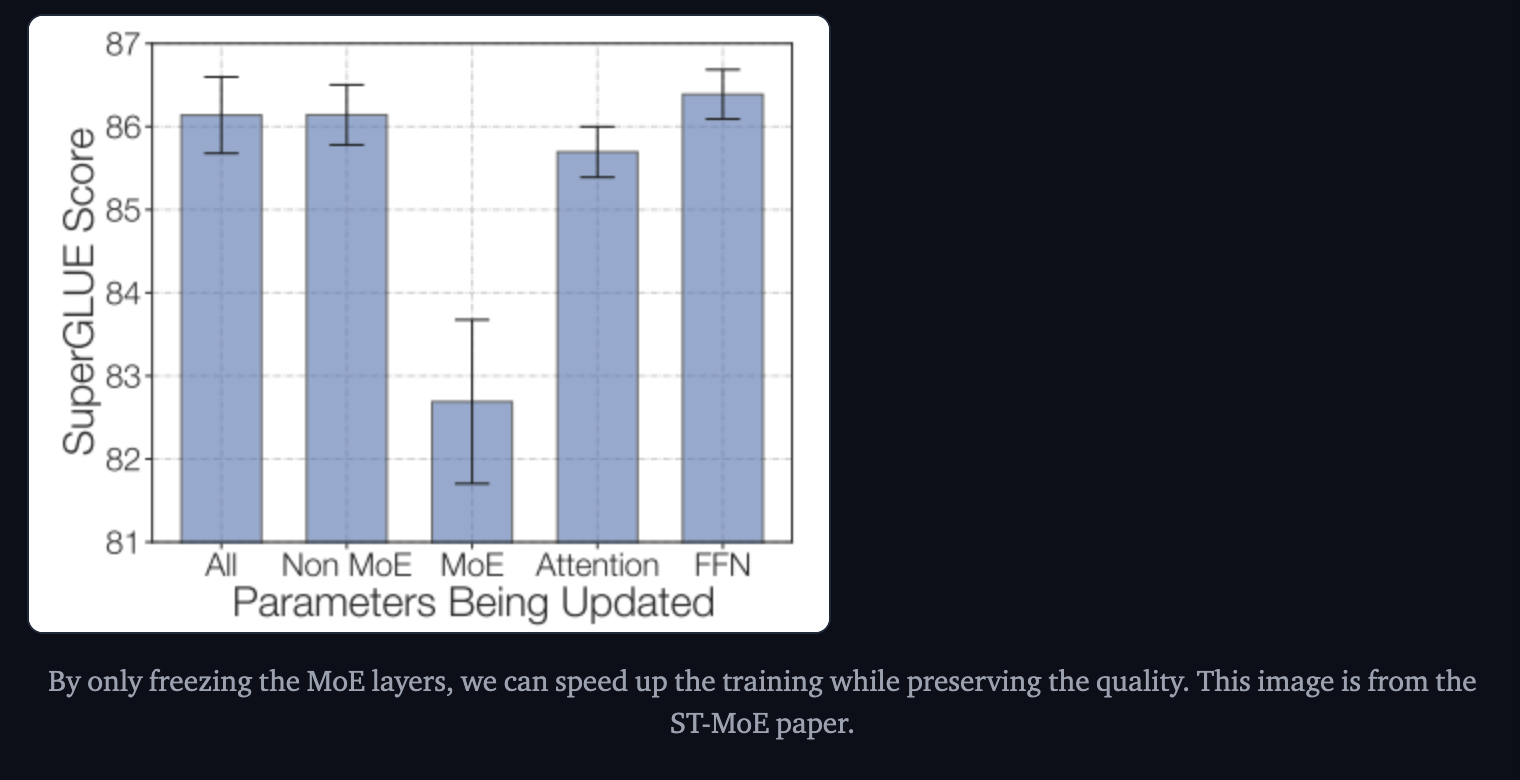
Freezing all non-expert weights and then finetuning leads to huge performance drop. However, the opposite, freezing only the MoE params worked almost as well as updating all parameters.

Sparse models tend to benefit more from smaller batch sizes and higher learning rates.

MoEs Meets Instruction Tuning(July 2023), performs experiments doing

1. Single Task Fine Tuning
2. Multi Task Instruction Tuning
3. Multi Task Instruction Tuning followed by Single task fine-tuning

They indicate the MoEs might benefit much more from instruction tuning. The auxillary loss is left on here, and it prevents overfitting

Experts are useful for high throughput scenarios with many machines

Making MoEs go brr

Parallelism

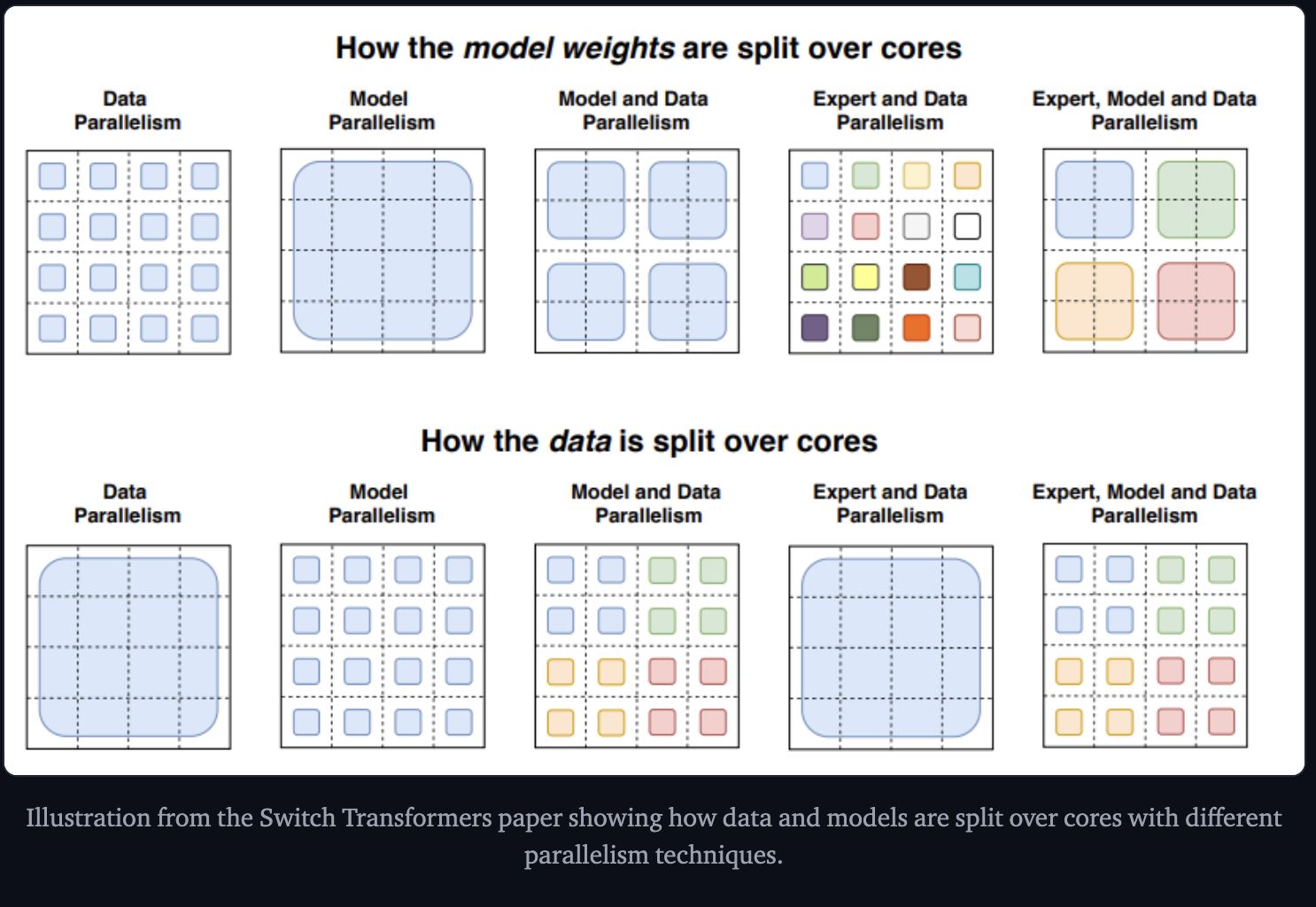
1. Data Parallelism - the same weights are replicated across all the cores and the data is partitioned across cores
2. Model Parallelism - The model is partitioned across cores, and the data is replicated across cores
3. Model and Data Parallelism - partion both across cores. Different cores process different batches of data.
4. Expert Parallelism - Experts are placed on different workers and each workes takes a different batch of training samples.
   

Capacity Factor

Increasing the capacity factor increases the quality but increases communication costs and memory of activations. A good starting point is using top-2 routing with 1.25 capacity factor and having one expert per core.

Serving Techniques

The Switch Transformers authors did early distillation experiments. By distilling a MoE back to its dense counterpart, they could keep 30-40% of the sparsity gains. Distillation hence provides the benefits of faster pretraining and using a smaller model in production.

There are approaches to modify the routing to route full sentences or tasks to an expert, permitting extracting sub networks for serving

Aggregation of Experts - Merges the weights of the experts, hence reducing the number of parameters at inference time.

Efficient Training

FasterMoE and Megablocks.