RoPE to YaRN

RoPE

Introduced in [1]

It encodes both the absolute position and the explicit relative position dependency.

It works with any high-dimensional space where the dimension is even.
It is given by

f_{q, k} (x_{m}, m) = R_{Θ, m}^{d} W_{q, k} x_{m}

Where

R_{Θ, m} = \begin{matrix} c o s (m θ_{1}) & - s i n (m θ_{1}) & 0 & 0 & . . . & 0 & 0 \\ s i n (m θ_{1}) & c o s (m θ_{1}) & 0 & 0 & . . . & 0 & 0 \\ 0 & 0 & c o s (m θ_{2}) & - s i n (m θ_{2}) & . . . & 0 & 0 \\ 0 & 0 & s i n (m θ_{1}) & c o s (m θ_{1}) & . . . & 0 & 0 \\ . . . & . . . & . . . . & . . . & . . . & . . . & . . . \\ 0 & 0 & 0 & 0 & . . . & c o s (m θ_{d / 2}) & - s i n (m θ_{d / 2}) \\ 0 & 0 & 0 & 0 & . . . & s i n (m θ_{d / 2}) & c o s (m θ_{d / 2}) \end{matrix}

Applying RoPE to self attention will show the emergence of the relative position data.

q_{m}^{T} k_{n} = (R_{Θ, m}^{d} W_{q} x_{m})^{T} (R_{Θ, n}^{d} W_{k} x_{n}) = x^{T} W_{q} R_{Θ, n - m}^{d} W_{k} x_{n}

By taking advantage of the sparsity nature of the matrix, there is a computationally efficient realization of the multiplication
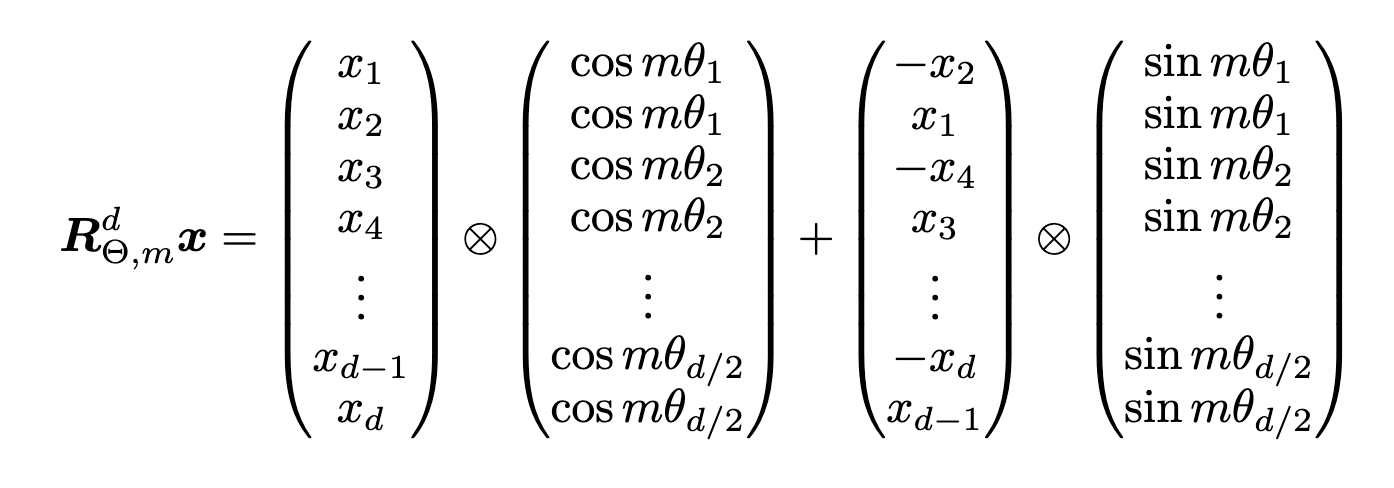
Pasted image 20251116154429.png

The authors have discovered that it converges faster than other strategies, but couldn't explain why.
RoPE also fails to generalize past the sequence length seen during training. Why is this the case?

Dimensions with low rotation angles experience unfamiliar attention angles when the attention window size is increased. For example, let's say we have a dimension that rotates 0.1 degrees per position, then for 768 positions, it would have rotated 76.8 degrees, but for longer sequences like 1024 tokens, it would rotate 102.4 positions, which the model wouldn't have seen during training
In the attention mechanism, when the K and Q vectors are normed, the perplexity of the attention mechanism increases as the number of keys increases. Applying a scaling factor helps here.

YaRN solves both of these issues!!

Position Interpolation

Introduced in [2]

A technique to extend the context window sizes.

Down-scales the Input Position Indices to match the original context window size, rather than extrapolating beyond the trained context length.

Finetuning an existing pre-trained Transformer to a longer context window, takes too many epochs, to give very small increase.

RoPE doesn't work well with extrapolation as well i.e the perplexity shoots up massively.

Instead of extrapolating, interpolate using the following

f^{'} (x, m, θ_{d}) = f (x, \frac{m L}{L^{'}}, θ_{d})

For common notation, We could write the above as follows:

f (x, g (m), h (θ_{d}))

with $g (m)$ and $h (θ_{d})$ taking appropriate values.

The ratio between the extended context length and the original context length,

s = \frac{L^{'}}{L}

NTK-Aware Interpolation

It was shown in [3], that deep neural networks have trouble learning high frequency information of the input dimension is low and the corresponding embeddings lack high frequency components.

Thus, uniform scaling results in a loss of high frequency details, which are needed for the network to resolve tokens that are both very similar and very close together.

Therefore, we have the following definition:

g (m) = m

h (θ_{d}) = b^{' - \frac{2 d}{| D |}}

and

b^{'} = b . s^{\frac{| D |}{| D | - 2}}

These functions basically are the ones defining the $m$ and $θ_{d}$ from the earlier equations in PI. So basically

NTK-by-parts Interpolation

Even when we do base change similar to what's shown above in the NTK-Aware Interpolation, all the tokes become close to each other. This makes it difficult to understand local relationships between tokens.

Thus a piecewise function is used.

g (m) = m

h (θ_{d}) = (1 - γ (r (d))) \frac{θ_{d}}{s} + γ (r (d)) θ_{d}

Where

r (d) = \frac{L}{2 π b^{' \frac{2 d}{| D |}}}

and

γ (r) = {\begin{cases} 0 & if r < α \\ 1 & if r \geq β \\ \frac{r - α}{β - α} & otherwise \end{cases}

YaRN

Yet Another RoPE Extension - It is a combination of the NTK-By-Parts with attention scaling.

Attention Scaling - Basically compute the following

s o f t m a x (\frac{q k}{t \sqrt{| D |}})

To achieve the following, scale the RoPE embeddings with $\sqrt{1 / t}$
$t$ is just a hyperparameter.

References

[1]

J. Su, Y. Lu, S. Pan, A. Murtadha, B. Wen, and Y. Liu, “RoFormer: Enhanced Transformer with Rotary Position Embedding,” Nov. 08, 2023, arXiv: arXiv:2104.09864. doi: 10.48550/arXiv.2104.09864.

[2]

S. Chen, S. Wong, L. Chen, and Y. Tian, “Extending Context Window of Large Language Models via Positional Interpolation,” Jun. 28, 2023, arXiv: arXiv:2306.15595. doi: 10.48550/arXiv.2306.15595.

[3]

Tancik, Matthew, et al. "Fourier features let networks learn high frequency functions in low dimensional domains." Advances in neural information processing systems 33 (2020): 7537-7547.